Understanding Quantum Gates
In classical computing, we use logic gates like AND, OR, NOT to manipulate bits (0 or 1). In quantum computing, we use quantum gates to manipulate qubits — not by flipping them, but by rotating their state on the Bloch sphere.
⚛️ Quantum gates are reversible and operate using unitary matrices, preserving probability amplitudes.
A single qubit state visualized on the Bloch sphere.
Common Quantum Gates
| Gate | Symbol | Effect | Matrix Representation |
|---|---|---|---|
| Hadamard (H) | H | Creates superposition: |0⟩ → (|0⟩ + |1⟩)/√2 | 1/√2 [[1, 1], [1, -1]] |
| Pauli-X | X | Bit-flip gate (like classical NOT) | [[0, 1], [1, 0]] |
| Pauli-Z | Z | Phase-flip gate — changes the phase of |1⟩ | [[1, 0], [0, -1]] |
| Controlled-NOT (CNOT) | ⊕ | Flips the target qubit if control qubit is |1⟩ | 4x4 Matrix |
Building a Quantum Circuit with Qiskit
# Simple Quantum Circuit Example
# pip install qiskit
from qiskit import QuantumCircuit, Aer, execute
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
# Create 2 qubits and 2 classical bits
qc = QuantumCircuit(2, 2)
# Apply gates
qc.h(0) # Superposition
qc.cx(0, 1) # Entangle qubits
qc.measure([0, 1], [0, 1])
# Draw the circuit
print(qc.draw())
# Simulate results
sim = Aer.get_backend('qasm_simulator')
result = execute(qc, sim, shots=1000).result()
counts = result.get_counts()
print("Measurement outcomes:", counts)
plot_histogram(counts)
plt.show()
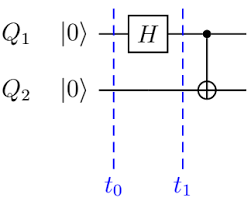
A Qiskit-style circuit that creates an entangled Bell state.
Visualization Tip
Use
Next → Quantum Algorithms
qc.draw('mpl') in Jupyter Notebook to render beautiful quantum circuit diagrams directly in-line!