Understanding Qubits

The Building Blocks of Quantum Information

What is a Qubit?

A qubit (quantum bit) is the smallest unit of quantum information — the equivalent of a bit in classical computing. While a classical bit can only be in one of two states, 0 or 1, a qubit can be in a combination of both states simultaneously, thanks to the principle of superposition.

💡 Mathematically: A qubit’s state can be expressed as
|ψ⟩ = α|0⟩ + β|1⟩ where α and β are complex numbers and |α|² + |β|² = 1

Visualizing a Qubit: The Bloch Sphere

The Bloch sphere is a 3D representation of a qubit’s state. The north pole represents |0⟩ and the south pole represents |1⟩. Any point on the sphere’s surface corresponds to a valid qubit state.

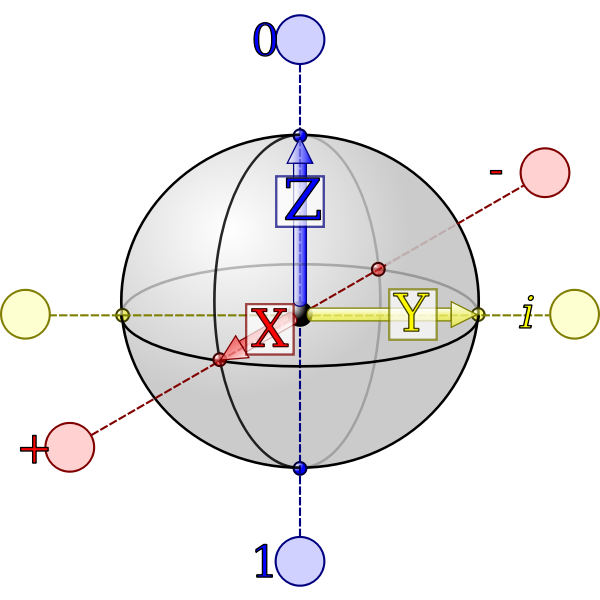
Bloch Sphere Representation

Visualization: A qubit in superposition on the Bloch sphere.

Superposition in Action

When we apply a Hadamard gate to a qubit initially in state |0⟩, it transitions into an equal superposition of |0⟩ and |1⟩. This means that until we measure the qubit, it’s effectively in both states. 


# Visualizing a Qubit on the Bloch Sphere
# pip install qiskit qiskit[visualization]

from qiskit import QuantumCircuit
from qiskit.visualization import plot_bloch_multivector
from qiskit.quantum_info import Statevector
import matplotlib.pyplot as plt

# Create a circuit with 1 qubit
qc = QuantumCircuit(1)

# Apply a Hadamard gate to create a superposition
qc.h(0)

# Get the statevector
state = Statevector.from_instruction(qc)

# Plot on the Bloch sphere
plot_bloch_multivector(state)
plt.show()

This visualization shows the qubit pointing along the X-axis of the Bloch sphere — halfway between |0⟩ and |1⟩ — representing an equal probability of measuring either outcome.

Measurement: Collapsing the State

Once a qubit is measured, its quantum state collapses to one of the basis states, |0⟩ or |1⟩. The probability of each outcome depends on the square of its amplitude (|α|² and |β|²). 


from qiskit import Aer, execute

# Add a classical bit for measurement
qc.measure_all()

# Simulate measurements
sim = Aer.get_backend('qasm_simulator')
result = execute(qc, sim, shots=1000).result()
counts = result.get_counts()

print("Measurement Results:", counts)

You’ll typically see results close to 50% 0 and 50% 1, reflecting the probabilistic nature of quantum systems.

🧠 Key Takeaway: A qubit doesn’t just hold data — it represents *probabilities and possibilities*. This is what gives quantum computing its exponential potential.

Next Concepts

Next → Quantum Entanglement